1.离散时间傅里叶变换DTFT
首先顾名思义,它的名字叫离散时间傅里叶变换,中间有个时间只是重在强调该变换仅在时域上离散,而在频率上是连续的。我们知道,采样后信号的频谱是采样前信号的频谱在频域上以采样频率fs进行周期延拓而成的,而要想从中恢复出原来信号,就需要对采样频率fs和有用信号的上限频率fo有一定要求,具体需要满足奈奎斯特采样定理,即要求 fs≥2fo ,而DTFT是对已采样信号求频谱的一种方式,公式的推导可以由采样的信号进行傅里叶变换得出。
DTFT正变换公式:\(\displaystyle X({e^{j\omega }}) = \sum_{n =-\infty }^\infty{x(n){e^{ - j\omega n}}}\)
DTFT逆变换公式:\(\displaystyle x(n) = \frac { 1 } { 2\pi }\int_{ - \pi }^{\pi} {X({e^{j\omega }}){e^{j\omega n}}} d\omega\)
具体可见下面推导。
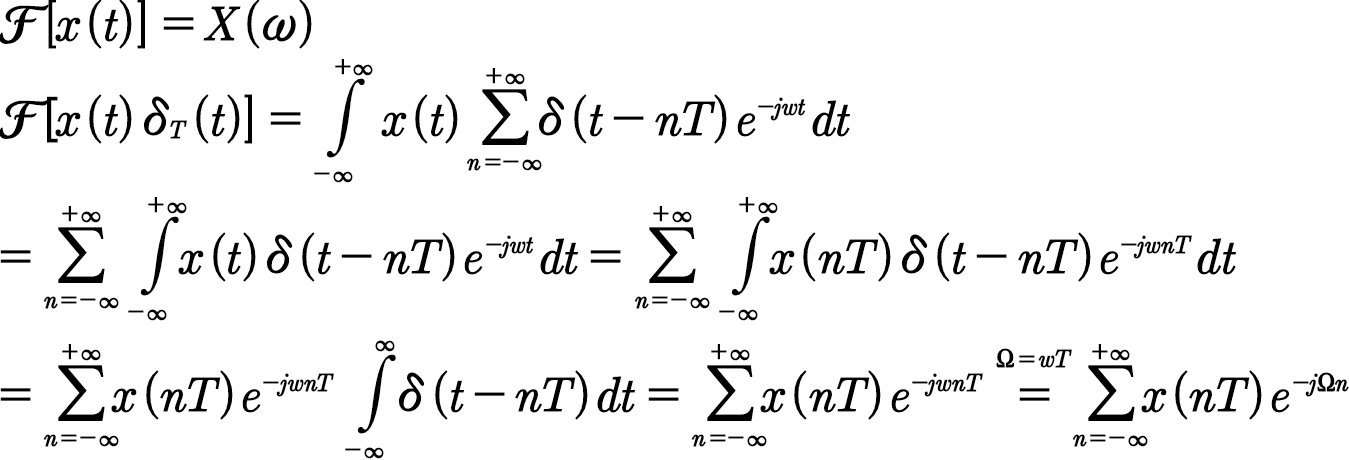
注意:对采样信号进行DTFT所得出的结果和我们进行频谱搬移得出的结果是一致的,只是从不同的角度得出的罢了,一个是从公式的角度计算出频谱,一个是以一个更为直观、更方便记忆的角度去分析的。
DTFT是具有周期性的,在数字角频率中,周期为2π,对应于模拟角频率时要乘以采样频率fs,即为Ωs,数字角频率可以看作是模拟角频率对采样频率的归一化,即ω=ΩTs,在学习数字信号处理的过程中,一定要区分好模拟角频率的数字角频率这两个概念,区分好了之后会发现很多都是相通的。
在学习信号的过程中,一定会不可避免的碰到周期与非周期信号、离散与连续信号,一般来讲,周期与离散是对偶的关系,而非周期与连续是对偶的关系。即时域周期的信号频谱是离散的,时域非周期的信号频谱是连续的,时域离散的信号频谱是周期的,时域连续的信号频谱是非周期的。
2.离散傅里叶变换DFT
说到DFT就不得提到DFS(离散傅里叶级数),DFS描述的是一个周期序列与它的傅里叶级数之间的变换,而DFT则取的是周期序列中的主值序列,因此,DFT隐藏着周期性。
-
2.1DTFT与DFT之间的关系
DFT正变换公式:\(X(k) = \sum\limits_{n = 0}^{N - 1} {x(n)W_N^{kn}}\) ( 0 ≤ k ≤ N - 1 ) 其中\(W_N^{kn} = {e^{ - j\frac{2\pi }{N}\omega n}}\)
从上面的公式我们可以看出,DFT变换是DTFT变换在【0,2π】区间上的N点等间隔采样,采样间隔为2π/N,详细解释可参考这里
-
2.2Z变换与DTFT、DFT之间的关系
Z变换公式:\(X(z) = \sum\limits_{n = - \infty }^\infty {x(n){z^{ - n}}}\)
同样的,从它们之间的公式可以看出,序列的DTFT变换是序列在单位圆上的Z变换,而序列的N点离散傅里叶变换是序列的Z变换在单位圆上的N点等间隔采样。
-
2.3DFT的应用
-
计算序列的线性卷积
我们知道线性卷积是离散时间信号处理的重要运算,如离散时间系统的时域响应就是通过系统的输入序列与系统的单位脉冲响应的线性卷积而得到的,但在时域上进行线性卷积效率是很低的,由于DFT和IDFT存在快速算法,因而利用DFT来计算线性卷积可以极大地提高计算地效率。
DFT是计算循环卷积的,时域循环卷积频域相乘,因此我们需要找到序列的循环卷积和线性卷积的关系,这里直接给出结论,假如单位脉冲响应h(n)的长度为N,输入序列的长度为M,当循环卷积长度L≥N+M-1时,循环卷积等于线性卷积。流程图可见如下。
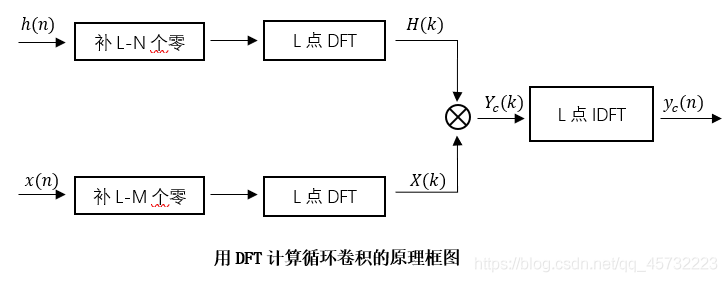
有限长序列与另一长度远大于其长度的序列进行卷积,如果按照上面直接用DFT计算的话,有两个问题。
①.必须知道无限长序列的全部元素,才能进行计算
②.用DFT计算卷积可能还不如直接进行卷积运算来得快
为解决上述的问题,可以将无限长序列划分为短序列,将短序列与有限长序列进行卷积,即进行分段卷积,然后对结果进行处理,主要由两种方法:重叠相加法和重叠保留法,这里就不细讲了,知道大致思路即可。
-
利用DFT对连续信号进行频谱分析
-
分析的过程
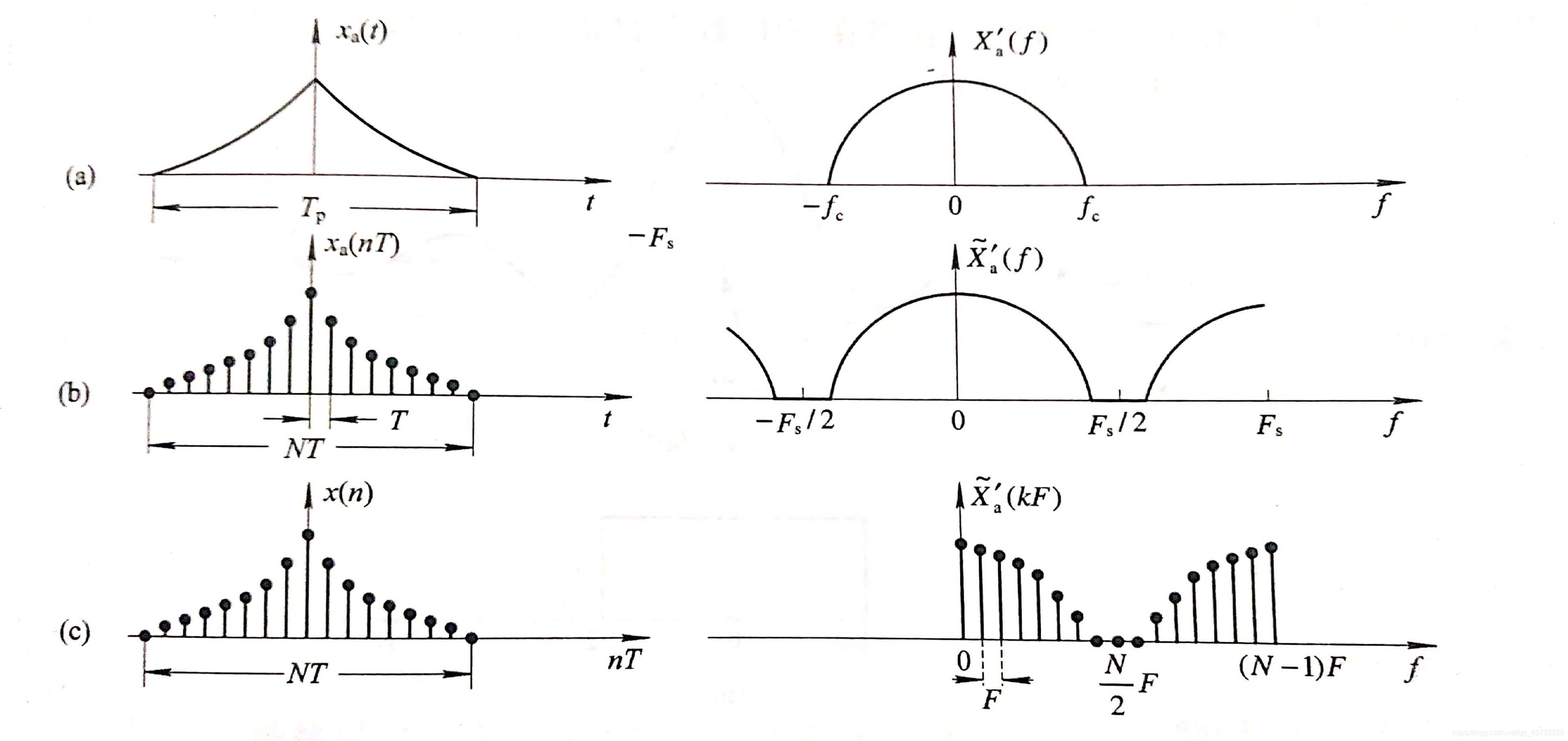
设连续时间信号为xa(t),其频谱函数Xa(jΩ)是Ω的连续函数。为了利用DFT对xa(t)进行频域分析,先对xa(t)进行时域采样,得到离散时间信号x(n)=x(nT),再对x(n)做DFT,得到的X(k)则是x(n)的离散时间傅里叶变换x(ejω)在频域【0,2π】区间上的N点等间隔采样。这里x(n)和X(k)均为有限长序列。然而,由信号的傅里叶变换理论知道,若信号持续时间有限长,则其频谱无限宽;若信号的频谱有限宽,则其持续时间无限长。所以严格地讲,持续时间有限的带限信号是不存在的。实际上对频谱很宽的信号,为防止时域采样后产生频谱混叠,应采用预滤波的方法滤除高频分量;而对于连续时间很长的信号,则往往来用截断的方法。过程如下。

从图中的频谱分析过程可以看出,利用DFT对连续时间信号进行频谱分析是一次一次近似的过程,其中每一次近似都会伴随有信息丢失,其近似程度与信号带宽,采样频率和截断长度等参数有关。
-
原理分析
大致的原理上面已经讲过,这里放张图,帮助回忆。
-
出现的问题以及解决方法
(1)频谱混叠
解决频谱混叠问题的唯一办法就是选择足够高的信号采样频率,这意味着通常需要知道原连续信号的频谱范围,以根据时域采样定理确定采样频率。然而在很多情况下无法预计信号的频率,为保证基本无混叠现象出现,一般在采样前利用模拟低通滤波器(也称抗混叠滤波器)对连续时间信号进行预处理(即预滤波),将其上限频率fmax限制在采样频率fs的一半以内,以减少混叠程度,提高频谱分析精度。
(2)截断效应
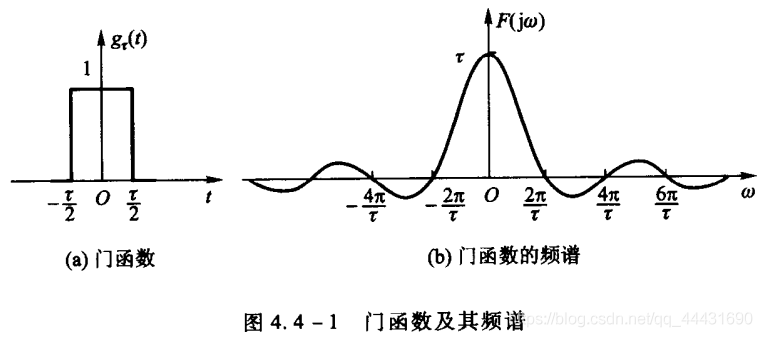
在xN(N) = x(n)RN(N)这个过程中会发生频谱泄漏(Rx(N)为矩形序列):因为RN(n)序列的DTFT是一个Sa()函数,时域的乘积对应频域的卷积,因此会发生频谱的泄露。
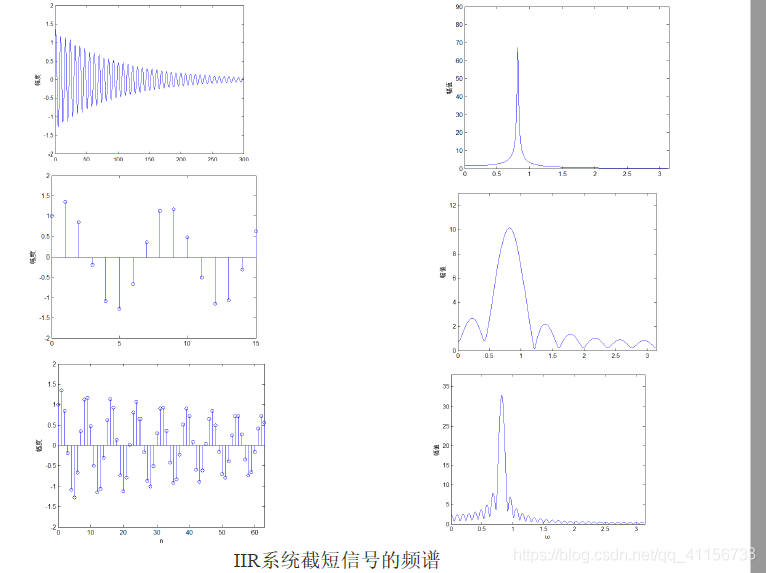
第二行图像是用N=16的矩形序列对原始信号x(n)进行截断的结果,左图为时域形状,右图为对应频谱。可以明显观察到:原始信号x(n)的频谱在Ω0处有一个尖峰,其他频率分量上几乎为0;但在N=16这幅图像中Ω0处的尖峰被扩展,一个周期几乎所有频率上都有非零值,即频率从Ω0处泄漏到其他频率处去了。
第三行图像是用N=64的矩形序列对原始信号x(n)进行截断的结果,左图为时域形状,右图为对应频谱。可以明显观察到:相较于N=16的图像,此时的频谱在Ω0处的尖峰更加明显,在其他频率上的分量较之也有明显的衰减。
由上图可见,无限长序列的加矩形窗截断后的频谱函数XN(ejω)与原序列频谱函数X(ejω)有差别。这种差别对频谱分析的影响主要表现在下面两个方面。
①.频谱泄漏
无限长的序列加矩形窗截断后,在矩形窗频谱函数的作用下,使得XN(ejω)出现较大的频谱扩展和向两边的波动,通常称之为频谱泄漏或功率泄漏,给频率分析带来了误差,使得频率分辨率降低。当一个大信号和小信号频率相近时,会淹没掉小信号。所以,在DFT变换区间(即截取长度)N一定时,只能以降低谱分析分辨率为代价,换取谱间干扰的减小。
②谱间干扰
截断引起的频谱展宽和波动,还会造成频谱混叠,即当他的高频成分超过ω=π(相当于折叠频率fs/2),不同频率分量信号间的频谱产生混叠现象,称之为谱间干扰,或者由于频谱混叠而产生较大的峰值,被误认为是另一个信号的谱线,从而造成虚假信号。
以上两种现象都是由于对长序列截断引起的,所以称之为截断效应。解决办法:
1.增加截断长度,增加截断长度会使主瓣宽度变窄,但主副瓣相对电平不变
2.选用副瓣较小的窗函数,如哈明(hamming)窗,汉宁(hanning)窗
关于窗函数及其频谱函数将在FIR滤波器设计中介绍。或者看这里
频谱泄漏和谱间干扰来源于窗函数和数字序列的乘积,是两个序列DTFT的卷积。理解频谱泄漏,要从DTFT的角度理解;DFT只不过是对DTFT的采样,与频谱泄漏无关。
(3)栅栏效应
我们知道,序列的N点DFT是在频域【0,2π】区间上对序列的DTFT做N点等间隔采样,而采样点之间的频谱函数值我们是不知道的。所以,用DFT来观察序列的频谱如同通过一个栅栏来观察景物一样,这样在一些频谱的峰值和谷点就可能被“栅栏”遮挡而观察不到,这称为栅栏效应。
减小栅栏效应的常用方法是在原序列的末端补零,再进行DFT变换。对序列末端补零之后,序列的DTFT不变,但是序列的DFT会对序列的DTFT的【0,2π】区间有更多的采样点数,从而将会显示更多细节。
-
参数选择
(1)频率分辨率
频率分辨率的定义是DFT频域相邻刻度之间的实际频率之差Δf,即为fs/N。
频率分辨率与栅栏效应是不同的两个概念。如果截取长度为N的一段数据序列,则可以在其后面补N个零,再进行2N点DFT,使栅栏宽度减半,从而减轻了栅栏效应。
但是,这种截短后补零的方法不能提高频率分辨率。因为截短已经使频谱变模糊,补零后仅使采样间隔变小,但得到的频谱采样仍是已经变模糊的频谱,所以频率分辨率没有提高。因此,要提高频率分辨率,就必须对原始信号截取的长度加长,也就是增大窗的宽度,在采样率不变下,就是增加采样时间Tp。
(2)采样频率
设连续时间信号的最高频率为fc,则信号的采样频率fs需满足,fs≥fc。
(3)信号的持续时间
信号的持续时间Tp应满足频率分辨率的要求,即Tp=1/Δf,即长的信号采样持续时间会得到较高的频率分辨率(即Δf越小)
3.快速傅里叶变换FFT
FFT只是一种快速计算DFT的算法,该算法的出现使得FFT被广泛的应用,主要原因就是旋转因子WNk具有周期性、对称性和可约性。最基本的原理为基2FFT算法,主要通过蝶形运算符号实现,完成一次蝶形运算,需要一次复数乘法和两次复数加法运算。