平面电磁波
电磁波根据其空间等相位面的形状分类为:平面电磁波、柱面电磁波、球面电磁波。严格来讲,平面电磁波其实是并不存在的,因为只有无限大的波源才能激励出这样的波。但是如果场点离波源足够远的话,那么空间曲面的很小一部分就十分接近平面,其传播特性也十分接近平面电磁波。在远离发射天线的接受点附近的电磁波,可以近似看成平面电磁波,如电基本阵子,在远场区,电场只有θ分量,磁场只有φ分量,E×H=r,即传播方向。
我觉得平面电磁波这个概念与光平行传播这个概念有点类似,我们把光近似看成平行传播是因为地球离太阳很远,太阳为源点,地球为场点,我们这样近似之后发现可以大大简化计算,而且带来的误差很小,于是便运用起来。
所谓均匀平面电磁波就是指等相位面为无限大平面,且平面上各点的场强大小相等、方向相同的电磁波,即沿某方向传播的平面电磁波的场量除随时间变化外,只与传播方向的坐标有关,而与其他坐标无关。
1 无耗介质中的平面电磁波
- 无耗介质中齐次波动方程的均匀平面波解
对于无耗介质,即满足 σ=0,而无源意味着无外加场源,即 ρ=0,J=0。(但是我有个问题,不是说 J=σE吗,σ=0不是可以推出 J=0吗?问题先留在这)
在无源、无界、无耗的简单介质中,对于传播方向而言,电磁场只有横向分量,没有纵向分量,这种电磁波被称为横电磁波(transverse electro-magnetic wave),或称为TEM波。TEM波的电场强度、磁场强度和传播方向(能流方向)三者构成右手关系。(E,H,S),三者叉乘满足循环关系,也即E×H=S,H×S=E,S×E=H。
这里我们为了简单,假设电场强度只有x分量,那么磁场强度只有y分量,因为我们假设电磁波是沿着z方向传播的。对于正弦电磁场,无源、无界、无耗的简单介质:
均匀平面波的电场强度可以解为 \(E\left( z \right) = \overrightarrow (E_0^ + {e^{ - jkz}} + E_0^ - {e^{ + jkz}})\),第一项为入射波,第二项为反射波,这表明电场强度仅有两个分量组成:入射波和反射波。对于不同的具体情况,电场强度的不同表现在入射波和反射波的比例不同。而均匀平面波的磁场强度为\(H\left( z \right) = \overrightarrow {a_y} \frac{1}{\eta }(E_0^ + {e^{ - jkz}} - E_0^ - {e^{ + jkz}})\),在这里,\(\eta = \frac{\omega \mu }{k} = \sqrt{ \frac { \mu }{ \varepsilon }}\),其由阻抗的量纲,它的值与介质参数有关,因此它被称为介质的波阻抗。真空中的介电常量和磁导率为 μ0= 4π × 10-7H/m,ε0= 1/36π × 10-9F/m。因此真空中的波阻抗为 \({\eta _0} = \sqrt {\frac{\mu _0}{\varepsilon _0}} = 120\pi \approx 377\)。
- 均匀平面波的传播特性
正弦均匀平面电磁波的电场和磁场在空间上相互垂直,在时间上是同相的,它们之间的振幅有一定的比值,取决于介质的介电常量和磁导率。 将它们化为瞬时值表达式后(分析入射波):
\[\begin{array}{l} {\bf E\left( {z,t} \right)} = \overrightarrow {a_x} {E_{om}}\cos (\omega t - kz + {\varphi _0})\\ {\bf H\left( {z,t} \right)} = \overrightarrow {a_y} \frac{E_{om}}{\eta }\cos (\omega t - kz + {\varphi _0}) \end{array}\]我们有以下定义:
(1) 相速
平面电磁波等相位面行进的速度称为相速,以vp表示,vp实际上是沿波阵面的法向等相位面移动的速度,我们可以由等相位面方程\(\omega t - kz = const\)导出 :
\[{v_p} = \frac{dz}{dt} = \frac{\omega }{k} = \frac{1}{\sqrt {\mu \varepsilon } }\](2) 波长
空间相位 kz 变化 2π 所经过的距离称为波长,以 λ 表示。kλ = 2π,所以:
\[\lambda = \frac{2\pi }{k}\]此时表明波长除了和频率有关外,还和介质参数有关。因此,在同一频率的电磁波,在不同介质中的波长是不同的。此外式还可写为:
\[k = \frac{2\pi }{\lambda }\]k 称为波数,因为空间相位 kz 变化 2π 相当于一个全波,k 表示单位长度内所具有的全波数目的 2π 倍;k 也被称为电磁波的相位常数,因为它表示沿传播方向上波行进单位距离时相位变化的大小。
(3) 周期
时间相位 ωt 变化 2π 所经历的时间称为周期,以 T 表示。而一秒内相位变化 2π 的次数称为频率,以 f 表示。
\[f = \frac{1}{T} = \frac{\omega }{2\pi }\]由以上关系可得 :vp= λf
小tips:η0 = μ c,初看这个公式没啥用,但是可以帮助我们计算出磁导率,从而算出真空中介电常数。
- 向任意方向传播的均匀平面波
对于任意传播方向的电磁波,复场量可以表示为\(\overrightarrow E = \overrightarrow {E_0} {e^{ - j\overrightarrow k \cdot \overrightarrow r }}\),其中\(\overrightarrow r = x\overrightarrow {a_x} + y\overrightarrow {a_y} + z\overrightarrow {a_z}\),为等相位面任一点的失径,其中\(\overrightarrow k = k\cos \alpha \overrightarrow {a_x} + k\cos \beta \overrightarrow {a_y} + k\cos \gamma \overrightarrow {a_z}\),它为传播矢量,它的模为 k 。
2 导电介质中的平面电磁波
- 导电介质中平面电磁波的传播特性
我们知道,介质在电磁场的作用下会表现出三种状态,极化、磁化和传导,分别对应介电常量、磁导率、电导率。这一节,我们分析有耗介质(\(\sigma \ne {\rm{0}}\))中平面电磁波。
在有耗介质中,我们引入导电介质的复介电常量,\({\varepsilon _{\rm{c}}}{\rm{ = }}\varepsilon {\rm{ - j}}\frac{\sigma }{\omega }\),这样在有损介质中的麦克斯韦方程和无耗介质中的麦克斯韦方程有相同的形式。因此波动方程中的\({k^2} = {\gamma ^2} = {\omega ^2}\mu {\varepsilon _c}\),然后我们把复数γ写成\(\gamma = \beta - j\alpha\),其中β称为相位常数,α为衰减常数,显然导体中,电场强度的振幅以因子\({e^{ - \alpha z}}\)随 z 的增大而减小。因此波阻抗 η 也为复数,这意味着电场强度和磁场强度在空间上仍互相垂直,但在时间上有相位差,电场强度相位超前于磁场强度。
而且,一个非常重要的点就是在导体介质中的平面电磁波的相速小于光速,且频率高,相速快,此外还和电导率有关,σ 越大,相速越慢。这样携带信号的电磁波其不同频率分量将以不同的相速传播,一段时间后,它们的相位关系将发生变化,从而导致信号失真,这种情况称为色散,所以导电介质为色散介质。
- 集肤深度和表面电阻
我们定义损耗角正切 \(\tan \delta = \frac{\sigma }{\omega \varepsilon }\),这是按照导电介质中传导电流振幅和位移电流振幅比值决定的。我们把 tanδ=0 的称为理想介质(无耗),把 tanδ=∞ 称为理想导体,把 tanδ»1 的称为良导体,把 tanδ«1 的称为良介质。
对于良导体来说,它的衰减常数近似为\(\alpha = \beta = \sqrt {\frac {\omega \mu \sigma }{2}}\),和频率、电导率有关,因此,高频电磁场只能存在于良导体的表面,这种现象称为集肤效应(skin-effect)。电磁场衰减到表面的1/e 的深度,称为集肤深度,以 δ 表示,δ = 1/α。
这一发现有很多应用,比如我们可以用金属片屏蔽电磁波,如晶体管的金属外壳,可以很好的屏蔽外部电磁场对其内部的影响。比如海水是良导体,要想和潜艇进行通信,一般使用低频电磁波,微波炉中不能使用金属盘子进行食物加热。
传入导体的电磁波实功率全部转化为热损耗功率。导体表面处切向电场强度和切向磁场强度之比定义为导体的表面阻抗\({Z_s} = {R_s} + j{X_s}\)。导体的表面阻抗等于波阻抗,\({R_s} = \sqrt {\frac {\omega \mu }{2\sigma }}\),Rs 和 Xs分别称为表面电阻和表面电抗。表面电阻相当于单位长度,单位宽度,厚度为集肤深度的导体块的直流电阻。导体的表面电阻所吸收的功率等于电磁波垂直传入导体所耗散的功率。
- 无耗一词的理解
注意:我之前一直以为理想导体的电阻率为0,不就没有电阻,不应该是无耗介质吗?怎么理想介质才是无耗的。原来我们这个无耗的耗是对电磁场的损耗,而不是导体因电阻发热而产生的损耗。理想导体内部的电场和磁场为0,对电磁场的损耗为无穷大。
3 电磁波的极化
定义:空间中某点电场强度的失端随时间变化的方式,即失端轨迹。通俗一点就是固定坐标z来观察电场随 t 的变化,一般取 z =0。
主要分为线极化,圆极化,椭圆极化。线极化的主要有对称阵子,单极子等,圆极化的主要有螺旋天线,螺旋天线主要有轴向模,
- 判断线极化的方法:
x分量电场与y分量电场同相或相差 π 。线极化分为水平极化和垂直极化,如果电场矢量平行于地面,那么就是平行极化,如果电场矢量垂直于地面,那么就是垂直极化。举个例子,例如广播天线,电视、调频广播和短波广播一般采用水平极化,那么它发射出的远区电磁波就是水平极化波,我们接受的时候要尽量使天线水平,比如经典的八木天线,此时我们称二者的极化状态匹配。而且任何极化波都可以由两个极化方向垂直的线极化波叠加。
- 判断圆极化的方法:
x分量电场与y分量电场的振幅相等,相位差 \(\pm \frac{\pi }{\rm{2}}\),如果\({\varphi _x} - {\varphi _y} = \frac{\pi }{2}\),则为右旋圆极化波,如果\({\varphi _x} - {\varphi _y} =- \frac{\pi }{2}\),则为左旋圆极化波。注意:在固定时刻,观察合成电场强度矢量的失端轨迹沿传播方向随空间坐标 z 的变化,那么它的大小和方向在垂直于传播方向的平面上的投影与固定空间坐标 z 而电场强度矢量的失端轨迹随时间 t 变化的方式相同,但是二者的旋向相反。极化的定义是固定坐标z来观察电场随 t 的变化,但我们经常固定时间 t 来观察电场随 z 的变化,但是二者极化方向相反,这就是固定时刻和固定坐标的问题。
圆极化是两个幅度相同、相位相反且空间正交的相干信号叠加而成,轴比就是这两个的比值。圆极化生成的条件:等幅、反相正交馈电,也正因此,沿着传播方向来看,电磁波合成电场矢量的末端扫出的轨迹就是一个圆。而如果等幅、正交相位的条件不满足,则就是椭圆极化,也就是末端扫出的轨迹是一个椭圆。
一个线极化波可以分解为两个振幅相等、旋向相反的圆极化波的叠加,所以不同取向的线极化波都可以由圆极化天线接收。
- 判断椭圆极化的方法:
其实椭圆极化为更一般的情况,如果\(\bf 0 < {\varphi _x} - {\varphi _y} < \pi\),则为右旋椭圆极化波,如果\(\bf - \pi < {\varphi _x} - {\varphi _y} < 0\),则为左旋椭圆极化波。
一个椭圆极化波可以分解为两个振幅不等、旋向相反的圆极化波。
- 交叉极化与主极化
交叉极化:交叉极化携带能量对主极化是一种损失,这里的主极化是什么呢,就是天线的主业,那么交叉极化就是不务正业了,,(与主极化相对的就是交叉极化)
- 圆极化的产生
1.螺旋天线可以产生圆极化电磁波
2.产生两个幅值相等、相位差90°、极化方向垂直的线极化波。相位差的产生可以使用四分之一波长的传输线。
- 极化的测量
这是我学微波时做的实验
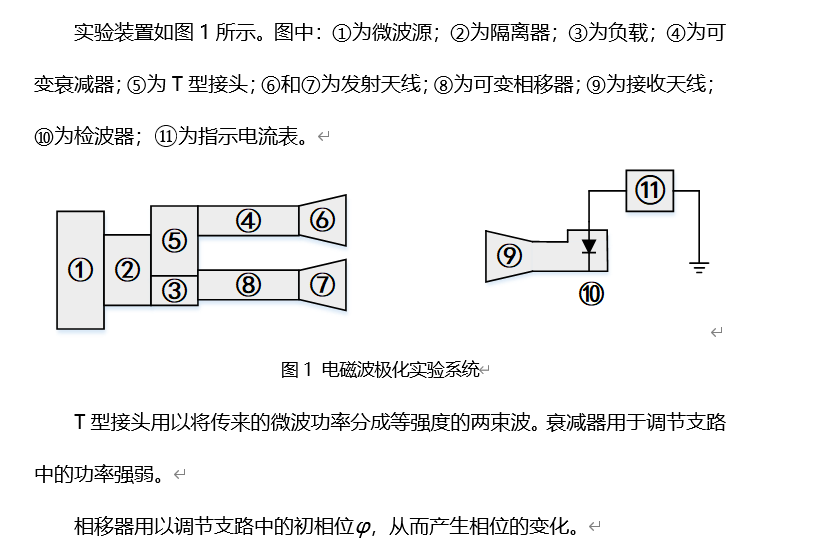
实验步骤:
使用电磁波极化系统测量电磁波的极化。
- 用金属板挡住发射天线6,转动接收天线9测出发射天线7的辐射图(线极化)。
- 用金属板挡住发射天线7,利用接受天线9测出发射天线6的辐射图(线极化)
- 发射天线6和发射天线7同时辐射,使接收天线9在水平方向和垂直方向指示相同(不同时可调节衰减器改变两束波的振幅使相等);使接收天线9在水平方向和垂直方向电磁波相位正交(将接收天线9转动45度,调节移相器,使电流表指示与水平和垂直相等),测其合成辐射图为圆极化。也可调节相移器测出不同的相移量时的椭圆极化图像。
简单来讲,就是通过旋转接收天线,根据电流来判断发射天线的极化形式,一般旋转180°,如果电流有0值还有最大值,那么就是线极化天线,如果电流值不变,那么就是圆极化波,如果有变化但没有0值,那么就是椭圆极化波。其实一般很难测到真正的圆极化波。
还有一个东西挺好玩的,那就是极化栅,那是由金属条组成像栅栏一样的东西。如果极化方向相等,那就全反射,如果极化方向相反,那就全透射,类似于光学中的偏振片。我们也可以通过旋转偏振片来判断电磁波的极化方向。